역전파는 해당 층과 연관되는 관계를 따라서 그래프를 계산하고, 그 경로에 있는 모든 변수값들을 저장해놓고 활용해야한다. 따라서 역전파는 순전파보다 훨씬 더 많은 메모리를 사용할 수 밖에 없다.
본 포스팅에서는 역전파의 원리에 대해서 이해하고자 링크된 페이지를 참고하여 작성한 글이다.
아래 플로우는 역전파 순서를 기준으로 작성한 것이며 해당 역전파계산과 관련된 순전파 계산을 함께 제시해서 역전파 계산 이해에 도움이 되도록 작성해보았다.
아래 그래프를 참고하며 계산을 따라가면 이해가 더 수월하다.

<순전파>
목적함수 J는 손실함수 L과 l2 norm 정규화항 s를 더한 정규화된 손실값이다.

<역전파>
J를 L과 s에 대해서 각각 미분해준다.
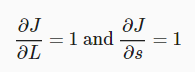
<순전파>
이전의 은닉벡터 h에 가중치 w2를 곱한 값인 o와 실제값 y의 손실값을 계산한다.

<역전파>
출력층 o의 변수들에 대한 목적함수 J의 미분값을 구한다.
J에 대한 L의 미분값 @ L에 대한 o의 미분값으로 계산한다.

<순전파>
정규화 항목으로 w1과 w2에 대한 l2 norm에 학습율인 람다/2를 곱해준다.

<역전파>
정규화항목에서 각 w1, w2에 대한 미분을 진행한다.
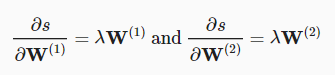
가중치 w2는,
J에대한 o의 미분 @ o에대한 w2의 미분값에
J에 대한 s의 미분 @ s에 대한 w2의 미분값을
더해서 구할 수 있다.

<순전파>
이전에 나온 출력층 z에 활성화함수를 적용한 히든 벡터 h에 가중치 w2를 곱해 출력층 o를 만든다.

<역전파>
은닉층 h에 대한 미분은
목적함수 J에 대한 o의 미분 @ o에대한 h의 미분값으로 구한다.

<순전파>
h는 z에 활성화 함수를 적용한 것이다.

<역전파>
출력층 z에 대한 미분은
J에 대한 h의 미분 @ h에 대한 z의 미분값으로 구한다.

<순전파>
입력값 x에 w1을 곱해 출력층 z를 만든다.

<역전파>
마지막으로 입력층과 가장 가까운 w1에 대한 미분을 진행한다.
J에 대한 z의 미분 @ z에 대한 w1의 미분값 + K에 대한 s의 미분 @ s에대한 w1의 미분값으로 구한다.

'Data > 머신러닝 & 딥러닝' 카테고리의 다른 글
| OOM (Out Of Memory) 해결 방법 (2) | 2022.01.27 |
|---|---|
| Custom Dataset tutorial - Fashion MNIST (0) | 2022.01.25 |
| 그레디언트와 경사하강법 (0) | 2021.08.06 |
| 심층 신경망 성능 향상시키기(3)/하이퍼파라미터 튜닝 (0) | 2021.08.04 |
| RNN과 게이팅 (0) | 2021.08.03 |