이번 포스팅에선 총 여섯가지의 이산확률분포를 정리하고, python의 scipy패키지를 통해 몇가지 그래프를 출력해보고자한다.
포스팅에서 다룰 여섯가지 분포는 다음과 같다.
- 베르누이 분포
- 이항분포
- 다항분포
- 포아송분포
- 기하분포
- 음이항 분포
▶ 베르누이분포 Bernoulli trial
베르누이 시행이란, 결과가 두가지 중 하나로만 나오는 실험이다.
베르누이 확률변수란, 두가지 중 하나로 나온 베르누이 시행의 결과를 실수 0 또는 1로 바꾼것을 말한다.
베르누이 분포란, 베르누이 확률변수의 분포를 일컫는다. 즉 시행횟수가 1번이고 한번의 시행결과가 성공(1) 혹은 실패(0)로만 나눠지는 분포를 베르누이 분포라고 한다.
▷ 분포함수
$$ P(x) = p^x(1-p)^{1-x}$$
- $x$가 0이면: P(0) = 1-p
- $x$가 1이면: P(1) = p
▷ 기호
$$B(1,p)$$
- 시행을 1번 수행할 때 성공확률은 P이다.
▷ 예시
주머니에 공이 10개 있고, 그 중 6개의 공은 빨간공(확률변수 0), 나머지 4개의 공은 파란공(확률변수 1)이라고 하자.
이 주머니에서 공 1개를 꺼낼 때 그 공의 색이 0일 확률은 0.6이다.
>주머니에서 나올 수 있는 결과는 빨간색, 파란색 공으로 두가지 뿐이며, 시행횟수가 한 번일 때의 확률변수 x의 분포를 나타낸 것이기 때문에 베르누이 확률분포이다.
▷ Scipy 코드
확률변수 1의 확률분포가 0.4인 베르누이 분포 시뮬레이션을 돌려보자.

rvs를 활용해 확률분포가 0.4인 random variates를 100개 만들어보자

위 변수의 분포를 그래프로 출력해보면 다음과 같다.

- 설정한 확률변수 1의 확률분포와 동일하진 않지만 유사한 분포의 시뮬레이션이 나오는 것을 볼 수 있다.
▶ 이항분포 Binomial distribution
서로 독립인 베르누이시행을 n번 할 때 사건이 발생한 횟수를 확률변수 x로 하는 확률분포를 말한다.
여기서 사건이 발생한 횟수는 베르누이시행의 성공횟수를 일컫는다.
즉, 이항분포는 서로 독립인 베르누이 시행에서 나오는 '성공'횟수의 분포라고 말할 수 있다.
▷ 분포함수
$$P(x)= _{n}C_{x} p^x (1-p)^{n-x}$$
- n번의 시행 중 순서와 상관없이 x번의 성공횟수를 선택한 경우의 수에 확률값을 곱해준다.
▷ 기호
$$B(n,p)$$
- 시행횟수가 n번일 때 성공 확률은 p이다.
▷예시
축구선수가 골을 넣을 확률이 70%라고 한다면, 그 선수가 10번 공을 찾을 때 성공횟수를 5라고 하자. 이때 해당 선수의 이항분포 값은 0.103정도의 값이 나온다.
$$B(10,0.7) = _{10}C_{5} 0.7^5 0.3^{5} = 0.1029$$
▷ Scipy코드
시행횟수가 10번이고 성공확률이 0.7인 확률 시뮬레이션을 돌려보자.
우선 예시에서 확률변수가 봤던 분포값이 맞는지는 다음 코드를 통해 알아볼 수 있다.
pmf 메소드를 통해 확률변수가 5일때의 이항분포 값을 출력해보았다.

- 공식으로 계산했을 때와 같은 값이 나온다.
이제 해당 분포를 갖는 무작위 변수를 100개 만들어보자.

- array에 들어간 값들은 10번의 시행 중 어떤 시행에서 성공이 나왔는지를 보여주는 값들이다.
[성공이 7번째 시행에서 나옴, 성공시행이 7번째 시행에서 나옴, 성공시행이 3번째 시행에서 나옴...]
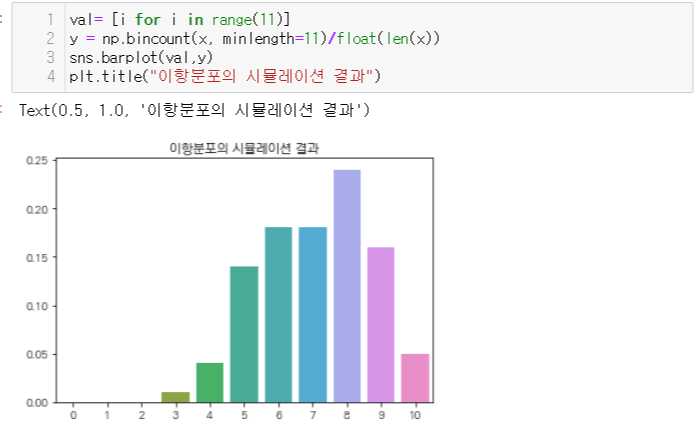
- 확률변수가 5일때를 기준으로 비교해보면 완전히 동일한 값은 나오지 않았다. 하지만 시뮬레이션 분포를 이론분포와 비교해보면 그와 비슷한 분포를 띈 그래프 모양일 것이다.
▶ 다항분포 Multinomial distribution
이항분포의 확장버전으로, 어떤 시행의 결과가 두개가 아니라 여러개로 나뉘었을 때의 분포이다.
다음 그림을 보며 이해해보자.
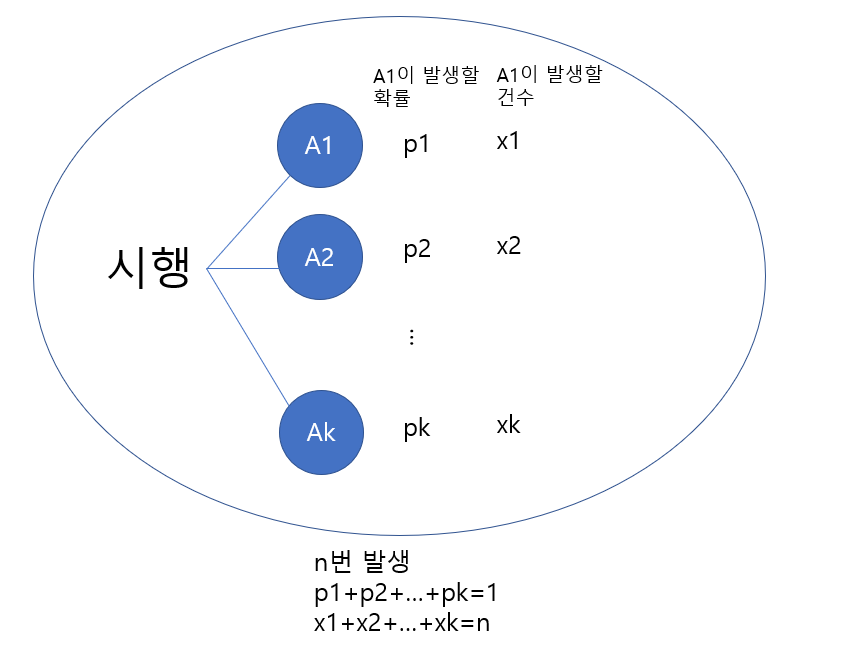
- 시행결과가 k라고 한다면 시행 결과는 $A_{1}, A_{2} ... A_{k}$로 k개의 사건으로 나눠진다.
- 각각의 사건에 대한 확률 또한 $p_{1},p_{2}...p_{k}$로 k개의 확률로 나눠질 수 있다. 이때 $p_{1},p_{2}...p_{k}$를 모두 더하면 1이 된다.
- 그리고 각각의 사건이 발생할 건수는 $x_{1},x_{2}...x_{k}$이고, 이들을 모두 더하면 n이 된다.
▷ 분포함수
$$P(x_{1},x_{2}...x_{k}) = \frac{n!}{(x_{1})!(x_{2})!...(x_{k})!}(p_{1})^{x_{1}}(p_{2})^{x_{2}}...(p_{k})^{x_{k}}$$
▷ 기호
$$M(n,p_{1},p_{2}...p_{k})$$
- n은 시행횟수, 각각의 p값은 각각의 사건이 발생할 확률이다.
▷ 예시
상자 안에 공이 100개가 들어있고, 빨간공 20개, 파란공 40개, 노란공 40개가 있다고 하자.
이 상자에서 복원 추출로 10개의 공을 뽑았다고 할 때, 그 10개 중 빨간공이 $x_{1}$개, 파란공이 $x_{2}$개, 노란공이 $x_{3}$개 들어있을 확률분포를 다항분포라고 한다.
▶ 포아송분포 Poisson distribution
- 어떤 단위시간동안 발생한 사건 횟수를 x라고 했을 때의 확률분포이다.
- 포아송 분포는 이항분포와 연관지어서 설명될 수 있다. 이항분포$B(n,p)$에서 시행횟수 n이 크고 성공확률p가 작은 경우에는 확률 계산을 정확히 하는것이 매우 어렵기 때문에 근사계산을 한다. 그리고 근사계산에선 np(정해진 시간안에 어떤 사건이 일어날 횟수에 대한 기댓값)의 값은 어떠한 양수 $\lambda$로 근사할 수 있다는 걸 전제하고 있다. 이 근사계산을 이항확률을 포아송근사라고 하고 이때의 확률분포를 즉 포아송 분포라고도 할 수 있다.
▷ 분포함수
$$ \lim_{n \to \infty,np_{n} \to \lambda}\binom{n}{x}p_n^x(1-p_{n})^{n-x} = \frac{e^{-\lambda}\lambda^x}{x!} $$
$$(\lambda >0)$$
- 포아송 분포는 이상분포에서 n이 무한대로, p가 0으로, np가 $\lambda$로 근사할 때의 분포이다.
▷ 기호
$$Pois (\lambda)$$
▷ 예시
DNA에 방사선을 쬐었을 때, 각 염기쌍이 돌연변이를 일으킬 확률은 각각 매우 작고 서로 독립적이다. 또한 하나의 DNA에는 많은 염기쌍이 있다. 따라서 DNA에 방사선을 쬐었을 때 발생하는 돌연변이의 개수는 푸아송 분포로 나타낼 수 있다.
▷ Scipy코드
정해진 단위시간에 어떤 사건이 발생할 횟수에 대한 기댓값을 $\lambda$라 했을 때, 그 사건이 x회 발생할 확률을 나타내보면 다음과 같다.
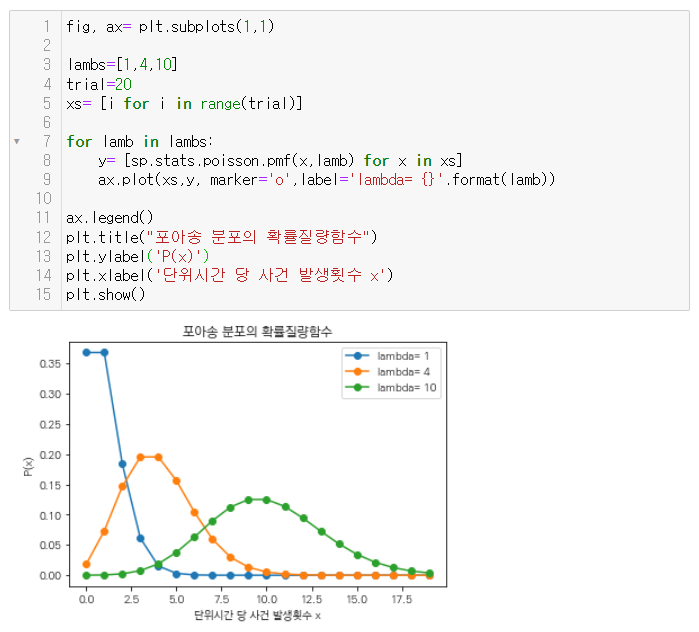
- lambda가 작을수록, 즉 사건이 발생할 확률이 적을수록 정해진 시간 내에 그 사건이 발생할 수 있는 횟수가 적을 확률이 더욱 크다.
- 반면 labmda가 클수록 정해진 시간 내에서 그 사건이 더 많이 발생할 확률이 커지는 것을 알 수 있다.
▶ 기하분포 Geometric distribution
성공 시행이 나오기까지 시행 횟수를 확률변수 x로 하는 확률분포이다.
여기서 각각의 시행은 서로 독립인 베르누이 시행이다.
▷ 분포함수
$$ P(x)= (1-p)^{x-1}p $$
- 성공확률이 p일 때 x번의 시행 중 실패한 시행은 x-1번 발생한다.
- 따라서 실패할 확률에 x-1승 한 값에 성공확률 p값을 곱해준 값이 확률변수 x에 대한 기하분포 값이다.
▷ 기호
$$ Geo(p) $$
▷ 예시
연애를 시작한 남녀가 결혼까지 갈 확률이 5%라고 하자.
이성을 사귈 때 그 이성과의 관계엔 결국 '결혼하냐 안하냐' 이 두가지 결과가 존재하기 때문에 이는 베르누이 시행이다. 이 예시에서 어떤 사람이 x번째 사귄 사람과 결혼할 확률분포가 기하분포이다.
즉, 세번째 사귄 사람과 결혼할 확률분포는 다음 식에 의해 0.125이다.
$$ P(3) = 0.5^20.5 = 0.125 $$
▷ Scipy코드
위 예시에 대해 파이썬으로 계산해보면 다음과 같다.

- 성공확률이 0.5인 베르누이 시행에서, 3번째 시행에 성공시행에 나왔을 경우의 기하분포 값
기하분포에서 성공확률에 따른 분포그래프를 그려보았다.
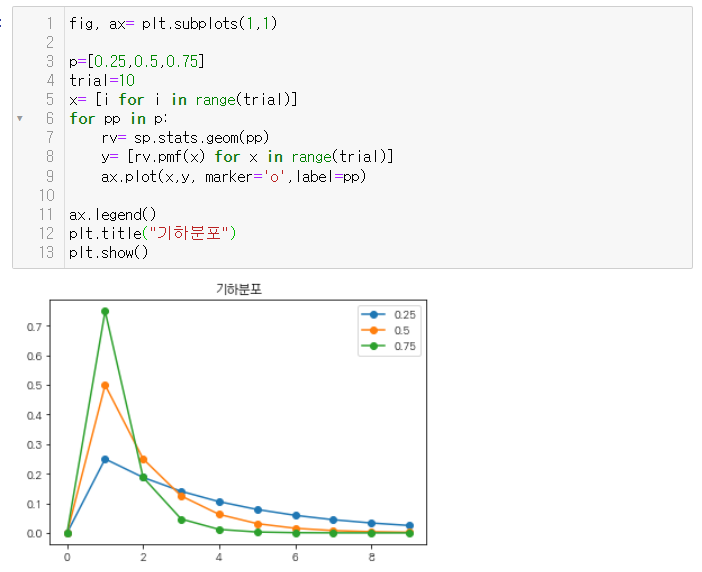
- 성공확률이 클수록 초반에 '성공'할 확률이 크고, 성공확률이 낮을 수록 초반에 '성공'할 확률이 낮다는 것을 알 수 있다.
▶ 음이항 분포 negative binomial distribution
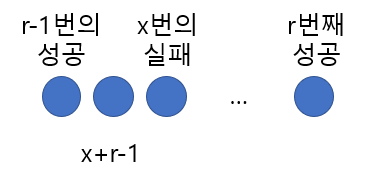
성공시행이 r번 나올때까지 실패한 횟수가 x회인 확률분포이다.
따라서, r번째 성공 전의 시행들 중에 실패시행은 x회가 들어있고 성공시행은 r-1회가 있다.
따라서 r번째 성공 전의 총 시행 수는 x+r-1회라고 할 수 있겠다.
▷ 분포함수
$$ P(x) = _{x+r-1}C_{x}p^r(1-p)^x $$
- $ _{x+r-1}C_{x} $ : r번째 성공 이전의 시행들이 나열될 수 있는 경우의 수
▷ 기호
$$ NB(r,p) $$
- 성공횟수 r, 성공확률 p
▷ 예시
어떤 농구선수의 자유투 성공확률이 30%라고 하자.
세번의 성공이 나오기까지 실패시킨 자유투 횟수가 x번일 때의 확률분포가 음이항분포이다.
즉, 세번의 성공이 나오기까지 자유투를 2번 실패시켰을 경우의 확률분포는 다음 식에 의하여 약 0.08이다.
$$ _{4}C_{2}0.3^3(0.7)^2 = 0.07938 $$
- r= 3, x=2, p=0.3
▷ Scipy코드
위 예시를 파이썬으로 계산해보면 다음과 같다.

10번 성공할때까지 걸리는 실패횟수 x에 대한 확률분포값을 성공확률에 따라 그래프로 출력해보았다.
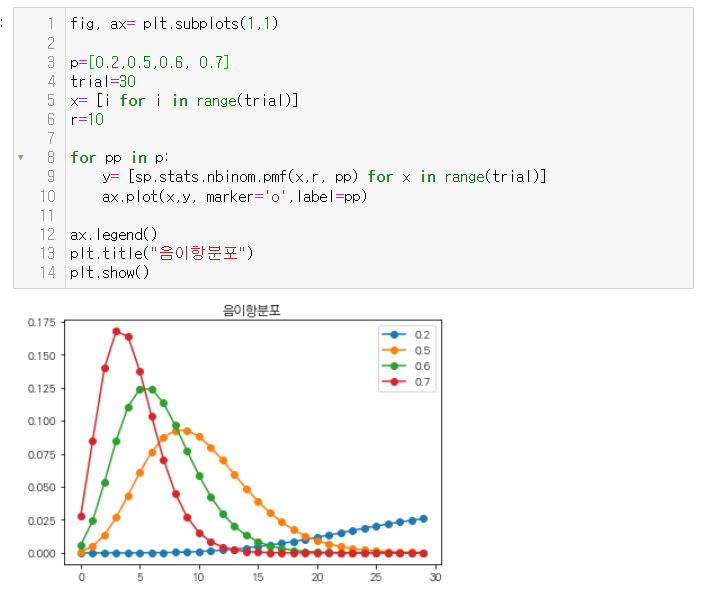
- 성공확률이 클수록 실패횟수가 적게 필요할 확률이 크다. 즉 성공확률이 클 수록 초기에 10번의 성공횟수를 채울 확률이 크기 때문에 그 과정에 들어갈 수 있는 실패횟수는 적어진다는 것을 알 수 있다.
- 반면, 성공확률이 작을수록 성공횟수 10번을 채우기까지 실패횟수가 많이 필요하고 대체적으로 분산도 큰 모습을 볼 수 있다.
▶ 참고자료
https://www.youtube.com/watch?v=CXum73zrMzc&list=LL&index=1
포스팅에서 틀린 부분에 대한 피드백 언제나 환영입니다!
'수학 > 통계학' 카테고리의 다른 글
| p-value란? / p-value 사용 시 주의할 점 (2) | 2022.01.28 |
|---|---|
| 정보이론 / entropy & Cross entropy & KL divergence (0) | 2022.01.20 |
| confusion matrix(혼돈행렬)과 TP,FP,FN,TN & Precision, Recall, f1-score에 대해 (0) | 2021.02.24 |
| 의사결정나무_분류모델 (0) | 2020.11.11 |
| 릿지회귀 RidgeRegression (0) | 2020.11.08 |