▶ Partial Dependence Plot이란?
기본적으로 tree기반의 모델은 선형회귀분석 같이 함수식을 통해 입력과 출력의 관계를 알기 힘들다.
tree기반 모델은 information gain을 기준으로 샘플을 부분집합으로 나누는데 집중하기 때문이다.
따라서 tree기반의 모델 중 하나인 RandomForest는 black box모델(어떻게, 무엇을 근거로 모델의 결과가 도출되었는지 알 수 없는 모델)까지는 아니지만 선형모델이나 일반 tree모델에 비해서는 해석이 어렵다.
PDP(Partial Dependence Plot)은 이러한 모델에서 입력과 출력의 관계를 알아볼 수 있도록 시각화하는 그래프이다. 이 그래프는 입력과 출력의 직접적인 관계를 추론하지는 않는다. 대신 하나 혹은 두 개의 변수가 예측 결과에 미치는 marginal effect를 보여주는 그래프이다.
더보기를 클릭하시면 marginal effect 정의를 보실 수 있습니다.
> marginal effect란?
marginal effect는 다른 모든 변수가 일정하게 유지되는 상황에서 한 변수에 변화가 생길 때, 이 변화가 결과 변수에 미치는 영향을 측정한다.
marginal effect는 변수를 marginalizing해줌으로써 구할 수 있다.
> marginalizing이란?
marginal distribution을 계산하는 과정이다.
아래 예시를 보자.

x 변수와 y변수의 각 확률분포중 빨간색 사각형 내 x의 확률변수 4칸, y의 확률변수 3칸의 값들이 각 변수의 marginal distribution이다. 즉, 확률변수 x의 marginal distribution을 구하기 위해 확률변수 y의 모든 값들을 더함으로써 marginalizing할 수 있다.
즉 PDP는 한 변수가 결과 변수에 어떤 영향을 미치는지 보여줄 수 있다. 다만 PDP역시 두 변수간의 상관관계를 보여주는 것이지 인과관계를 보여주는 것은 아니라는 점을 기억하자.
▶ PDP 원리 이해하기
PDP는 추이를 보고싶은 특정 변수를 제외한 나머지 변수들을 marginalizing해줌으로써 특정 변수가 결과 변수에 미치는 영향을 보여준다. 즉 다른 변수들에 대한 marginalizing과정을 통해 우리는 오직 특정변수와 결과변수만의 관계를 알아낼 수 있다.
▷ Regression에서의 partial dependence함수의 정의는 다음과 같다.

- xs: 결과변수와의 관계를 살펴볼 변수로 PDP plot으로 그려질 변수이다. 하나 혹은 두개의 변수가 될 수 있다.
- Xc : 학습이 완료된 머신러닝 모델 ˆf 에서 xs변수를 제외한 다른 변수들이다.
- ˆf(xs,Xc) :우리는 Xc 에 대해 marginalizing을 수행함으로써 set S가 결과변수에 미칠 영향을 알 수 있다. Regression에서는 Xc 와 xs 변수를 통해 머신러닝 결과값을 얻을 수 있다. 그리고 그 결과 값에 대해 dP(Xc)에서 Xc의 확률분포 값에 대해 적분함으로써 marginalizing을 해준다.
▷ 위 공식은 이론적인 공식이고 실제 컴퓨터 상에서는 다음과 같이 몬테카를로 방법을 적용한 공식을 따른다.

- n : instance의 개수
- 1n∑bi=1ˆf(xs,x(i)c) : 관심변수인 xs를 고정시킨 후 관심변수가 아닌 아닌 변수들인 x(i)c에선 모든 instance에 대한 평균값을 구한다.
예를 들어, 다음과 같은 데이터 셋이 있다고 할 때, 관심변수를 'hour'로 두면 다른 모든 변수는 xc로 들어간다.
공식에 따르면 hour가 20일 때 pd를 다음과 같이 구할 수 있다.
(다른 모든 변수들의 0번째 값과 hour=20 변수에 대한 모델 결과값 + 다른 모든 변수들의 1번째 값과 hour=20 변수에 대한 모델 결과값 + ... + 다른 모든 변수들의 20번째 값과 hour=20 변수에 대한 모델 결과값) / 20

위와 같은 과정을 hour가 13일때, 6일 때 ... 동일하게 수행해서 전체 partial dependence값을 알 수 있다.
즉 xs의 값에 변화를 줘서 모델의 결과값이 어떻게 변하는지 관측해 partial dependence값을 구할 수 있다.
다만, 위 공식은 우리의 관심변수인 xs가 다른 모든 변수들과의 상관관계가 없다는 가정 하에 사용할 수 있다는 점을 기억해야한다.
▶ PDP 예시
▷ 자전거 대여 예측 모델
아래 그림은 세가지 변수가 각각 자전거 대여 수에 어떤 영향을 미치는 지 보여주는 pdp예시이다.
자전거 대여 수를 예측하는 RandomForest모델을 적용해 도출된 결과를 시각화한 그래프이다.

- Temperature변수에선 온화한 기온(대략 15~25도 사이)일 수록 자전거를 많이 대여한다는 것을 알 수 있다.
- Humidity나 Wind speed의 경우, 해당 변수의 값이 높을 때는 자전거 대여율이 낮아진다는 것을 알 수 있다.
- 위 그래프를 해석할 때 주의해야할 것은 아래 나와있는 instance의 빈도를 봐야한다는 것이다.
wind speed의 pdp에서 노란색으로 표시된 부분의 그래프는 풍속이 약 25~35km/h쯤엔 자전거 대여 수에 변화가 없다고 나타내고 있다. 그러나 x축에 위치한 데이터의 빈도수를 보면 해당 부분에 대한 데이터의 빈도수가 많지 않다는 것을 볼 수 있다. 즉, 해당 부분에선 데이터가 적어 모델에서 의미있는 예측을 하지 못했기 때문에 그러한 결과가 나타났다는 것을 알 수 있다.
▷ 자궁경부암 분류 모델 1
아래 그림은 'Age'와 'Years on hormonal contraceptives'변수가 암 발병 확률에 어떤 영향을 미치는지 보여준다.
마찬가지로 RandomForest모델을 사용해 각 변수가 암 발병여부에 어떻게 영향을 미쳤는 지를 시각화한 그래프이다.
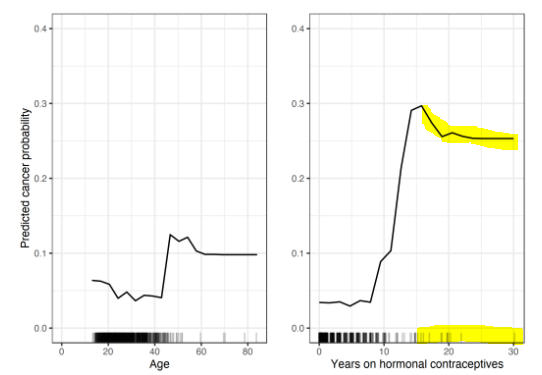
- age변수에선 40세 이하에서 암 발병 확률이 낮다는 것을 알 수 있다.
- Years on hormonal contraceptives 변수에선 피임약 복용 기간이 길수록 발병확률이 높아진다는 것을 알 수 있다.
- 그러나 해당 그래프에서 역시 해석 시 데이터 빈도 수를 고려해야한다. 두 변수 모두 값이 높아질 수록 데이터 빈도수가 낮아지므로 낮은 빈도수를 기록하는 구간에서의 그래프는 신뢰성이 낮은 구간임을 알고 있어야 한다.
▷ 자궁경부암 분류 모델 2
위와 같은 모델에서 두개의 관심변수들에 대해 출력한 pdp 예시이다.
두개의 feature을 가진 경우 아래와 같이 feature map을 통해 표현할 수 있다.
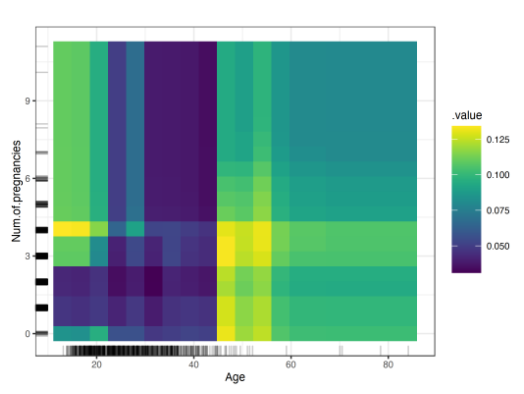
- 약 45살 부터 자궁경부암 확률이 증가하는 것을 볼 수 있다.
- 25살 미만의 여성들 중 임신을 한번 혹은 두번 경험한 여성일수록 발병확률이 높다는 것을 알 수 있다.
▶ PDP의 장점과 단점
▷ 장점
- 직관적이다 : 개념을 이해하는 것이 어렵지 않다. 또한 plot의 해석 역시 직관적으로 할 수 있다.
- 구현하기 쉽다: 관심 변수에 대해 marginalizing만 수행하면 된다.
▷ 단점
- 그릴 수 있는 변수개수가 한정되어있다: 하나의 plot에 그려서 직관적으로 해석가능한 변수의 개수는 2개까지라는 한계가 있다.
- 데이터 분포에 따른 해석오류의 여지가 있다: 데이터 분포에 따라 산출된 그래프가 잘못 해석될 수 있다. 데이터 분포가 적은 구간의 그래프를 해석할 땐 유의해야 한다.
- 다중공선성 문제가 없어야한다: 변수들간 상관관계가 없을 때 정확한 값을 산출할 수 있다.
- 여러 효과들이 무시될 수 있다: 임의의 고정된 xs에 대해 xc의 값들의 평균을 취해주었기 때문에 각 n개의 점들이 갖는 분포가 무시된다.
모든 instance들 중 반개의 값들은 예측결과에 긍정적인 영향을 주고 다른 반개의 값들은 결과에 부정적인 영향을 준다고 가정해보자. 이 때 두 값들이 서로 상쇄되어 PDP는 수평선을 그리게 될 것이다. 이 경우 우리는 해당 변수가 결과에 아무런 영향이 없다고 결론 내릴 수 있다.
이 단점을 해결하기 위한 방법으로는 Individual Conditional Expectation (ICE) plot이 있다. 해당 그래프에서는 모든 n개의 값들을 그래프에 표시해서 추이를 확인할 수 있다.
▶ Reference
Marginal distribution - Wikipedia
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables in the s
en.wikipedia.org
https://christophm.github.io/interpretable-ml-book/pdp.html
8.1 Partial Dependence Plot (PDP) | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'Data > 머신러닝 & 딥러닝' 카테고리의 다른 글
| Object Detection model - R CNN부터 Fast(er) R CNN까지 (0) | 2022.02.10 |
|---|---|
| CNN 모델 훑어보기 (0) | 2022.02.08 |
| OOM (Out Of Memory) 해결 방법 (2) | 2022.01.27 |
| Custom Dataset tutorial - Fashion MNIST (0) | 2022.01.25 |
| 순전파와 역전파 (0) | 2022.01.20 |