밑바닥부터 시작하는 딥러닝을 교재로 한 유튜브 강좌와 파이토치로 배우는 자연어처리 책을 참고하여 작성하였습니다.

▶ 퍼셉트론이란?
뉴런을 본떠 만든 가장 간단한 신경망으로 구성요소로 입력x, 출력y, 파라미터로는 가중치w와 절편b가 있다. 신경망의 기초가 되는 부분이기 때문에 해당 개념에 대해 짚고 넘어갈 필요가있다.
가중치와 절편은 데이터를 학습하면서 계속 업데이트 되는 파라미터들로, 가중치는 해당 입력값이 얼마나 중요한지를 나타내고 절편(=편향)은 임계값 역할을 하여 학습데이터와 가중치를 계산한 값이 해당 절편을 넘어야 하는 값이 된다. 따라서 편향이 높으면 높을 수록 입력값이 True가 되는 장벽이 더 높아진다고 할 수 있다. 아래 그림에서 편향은 -theta로 표현할 수 있다.

수학적으로 퍼셉트론은 다음과 같이 나타낸다.

일반적으로 퍼셉트론에는 1개 이상의 입력값 x가 들어간다. x는 입력 벡터, w는 가중치 벡터로 둘의 곱은 점곱으로 나타낼 수 있다.
x와 y에 따른 w와 b를 학습하는 함수인 활성화 함수 activation function은 타깃출력과 신경망을 기반으로 모델 설계자에 의해 결정된다.
▶ 논리게이트
퍼셉트론을 통해 논리 gate를 어떻게 표현할 수 있을지 보자.
▷ AND 게이트
AND 게이트는 아래와 같이 두 입력값이 모두 1일 때만 1을 반환하는 게이트이다.
해당 논리값이 구현되려면 퍼셉트론에서 임계값, 가중치들은 어떤 값을 넣어야 할까?

임의적으로 해당 게이트를 구현할 수 있는 주황색 값들을 사용하여 연산해보았다. 이 값들이 어떻게 나올 수 있는지 기하학적으로 확인해보자.
가중치값과 임계값을 활용해 식을 세워보면 다음과 같다. 가중치와 입력값을 점곱한 값이 임계값을 넘는 모양이다.

위 식을 그래프로 나타내면 다음과 같다.

(1,1)만 True가 될 수 있도록 직선그래프가 점들을 나눠주고 있다. 즉 and게이트는 위와 같은 점분리 형태를 가지도록 만드는 직선의 가중치와 임계값들이 적절한 값들이 될 것이다. 따라서 가중치 1/1.4말고도 적합한 가중치값으로 1/1.1, 임계값으로 1이 와도 and게이트를 구현할 수 있을 것이다.
▷ NAND게이트
NAND게이트는 AND게이트와 완전히 반대되는 논리값으로 두 요소가 모두 1일 때만 0을 반환하는 게이트이다.
위 게이트와 마찬가지로 논리값을 적절히 분리할 수 있는 임의의 가중치와 임계값을 구해 다음과 같이 구현할 수 있다.

위의 값들을 대상으로 그래프를 그려보면 다음과 같다.

AND게이트에서 부호값만 바꾸면, 즉 그래프를 원점을 기준으로 뒤집어주면 NAND게이트를 구현할 수 있다.
▷ OR게이트
OR게이트는 들어온 입력값 둘 중 하나라도 1이면 1을 반환하는 게이트다.

마찬가지로 임의로 주황색 값들을 가중치와 임계값으로 넣으면 게이트를 구현할 수 있는데 AND, NAND게이트의 임계값보다 임계값이 낮게 잡힌것을 알 수 있다.
이는 아래 그래프를 보면 그 이유를 쉽게 이해할 수 있다.

점들이 (1,0), (0,1)이 그래프의 위로 위치하는 직선그래프를 그려야하기 때문에 가중치가 임계값이 그 이전의 그래프의 임계값들보다 작게 설정되어야 게이트를 구현할 수 있는 것이다.
▷ XOR게이트
입력한 두 값이 서로 다를때만 1을반환하는 게이트이다.

위 세개 게이트는 하나의 직선으로 게이트를구현할 수 있었다. 하지만 이 게이트는 하나의 직선으로 점들을 분리시킬 수 없다. 즉 단층 퍼셉트론으론 구현할 수 없는 게이트이다.

이 점들을 분리 시키기 위해선 여러개의 단층 퍼셉트론이 필요하다. 우리는 이를 위 3개 퍼셉트론을 층층이 쌓아 구현할 수 있다.

위 그림과 같이 NAND와 OR게이트에서 나온 결과값들에 대해 다시 AND게이트를 실행해주면 XOR게이트 구현이 가능하다.
예를들어 1,0이 입력으로 들어가면 nand에선 1을 반환한다. or에서는 하나의 1이 존재하므로 마찬가지로 1을 반환한다. 두 게이트를 통해 나온 결과값인 1과 1을 AND게이트의 입력값으로 다시 넣어주면 두 입력값 모두 1이므로 결과 적으로 1을 반환한다.
지금까지 가장 간단한 신경망 모형인 퍼셉트론과 논리 게이트를 통해 퍼셉트론이 어떻게 작동되는지를 간단히 알아보았다.
지금부턴 논리게이트를 파이썬으로 어떻게 구현할 수 있는지 보자.
▶ AND, NAND, OR, XOR 게이트 구현

두개의 입력값을 받아 임의의 가중치와 임계값을 입력한 후 가중치와 입력값들을 각각 점곱해준다. 점곱한 값들을 모두 더한후 편향을 더해준 값이 0보다 작거나 같으면 0을, 0보다 크면 1을 반환하도록 한다.
나머지 NAND,OR 게이트 들도 가중치와 편향을 다르게 두고 구조는 동일하게 하여 작성한다.

XOR gate는 위에서 만든 세개 게이트의 함수를 사용하여 구현할 수 있다.
구현한 게이트들이 잘 작동하는지 확인해보자.

윗부분에서 설명한대로 논리값이 잘 도출되었다.
▶ 파이토치를 통한 구현
이번에는 파이토치를 활용하여 논리게이트를 구현해보자. 위에서는 우리가 게이트가 적절한 논리값을 도출할 수 있는 가중치와 편향을 직접 넣어줬지만, 이번엔 입력값과 반환값만 주고 모델이 학습을 진행하며 적합한 가중치와 편향을 찾아 값을 올바르게 예측하도록 학습하는 방식이다.

입력값과 출력값을 주고 퍼셉트론의 선형함수 wx+b를 구현할 수 있는 Linear함수를 사용한다. Linear함수의 파라미터값으론 들어오는 input값의 크기 2와 출력할 값의 크기1을 넣어주고 편향을 학습할 수 있도록 설정한다. 활성화함수로는 시그모이드를 사용하고 두 층을 묶어서 model로 만든다.
0과 1 두개의 값을 예측하므로 손실함수는 Binary Cross entrophy로 설정하고 가중치와 편향을 업데이트 시키는데 사용하는 optimizer로는 SGD를 사용하였다.
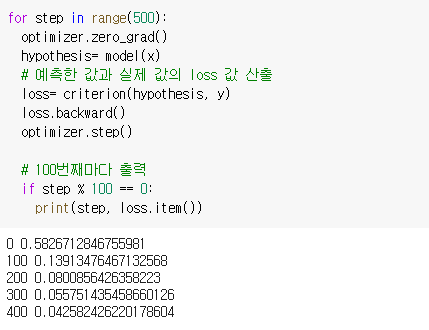
optimizer는 학습이전에 0으로 초기화 시켜준다. model의 입력값으로 x를 넣고 linear와 sigmoid 층을 통과해 산출된 출력값이 hypothesis에 저장되도록 한다. hypothesis와 y값에 대한 손실을 계산한 후 해당 손실을 매개로 역방향 계산을 수행하고 optimizer를 갱신시켜준다.
학습이 진행됨에따라 loss가 점점 줄어드는 것을 볼 수 있다.

학습된 가중치와 편향을 기준으로 산출된 예측값들을 보면 AND게이트가 잘 학습되었다는 것을 알 수 있다.
AND, NAND, OR 게이트는 같은 방식으로 작동하고 다층 퍼셉트론이 필요한 XOR 게이트도 파이토치를 활용해 구현할 수 있다. 이는 다음 링크 영상을 참고하자.
https://www.youtube.com/watch?v=f-EtWNybRoI&list=PLQ28Nx3M4JrhkqBVIXg-i5_CVVoS1UzAv&index=13
파이토치를 사용해 AND게이트를 구현하기 위해 시그모이드 활성화 함수와 cross entrophy 손실함수 등을 사용하였다. 해당 함수들에 대한 내용은 다음 포스팅에 정리해보았다.
'Data > 머신러닝 & 딥러닝' 카테고리의 다른 글
| 신경망의 기본 구성 요소(6)/ 손실함수 (2) | 2021.07.20 |
|---|---|
| 신경망의 구성요소(5)/ 활성화 함수- 소프트맥스 (0) | 2021.07.20 |
| 신경망의 구성요소 (4)/ 활성화 함수- ReLU (0) | 2021.07.20 |
| 신경망의 기본 구성요소(3)/ 활성화 함수- 하이퍼볼릭 탄젠트 (0) | 2021.07.19 |
| 신경망의 기본 구성요소(2)/ 활성화함수- 시그모이드 (0) | 2021.07.19 |