파이토치로 배우는 자연어처리 책과 참고하여 작성하였습니다.

▶ 하이퍼볼릭 탄젠트
하이퍼볼릭 탄젠트 활성화 함수는 시그모이드 함수를 선형변환한 것으로 시그모이드의 단점(그래디언트 소실)을 보완해주는 활성화 함수이다.
다음은 탄젠트의 공식이다.

탄젠트 활성화 함수는 시그모이드 함수를 선형변환한 것으로 다음과 같이 증명할 수 있다.

▷ 구현
하이퍼볼릭 탄젠트 활성화 함수를 파이토치로 구현해보자.
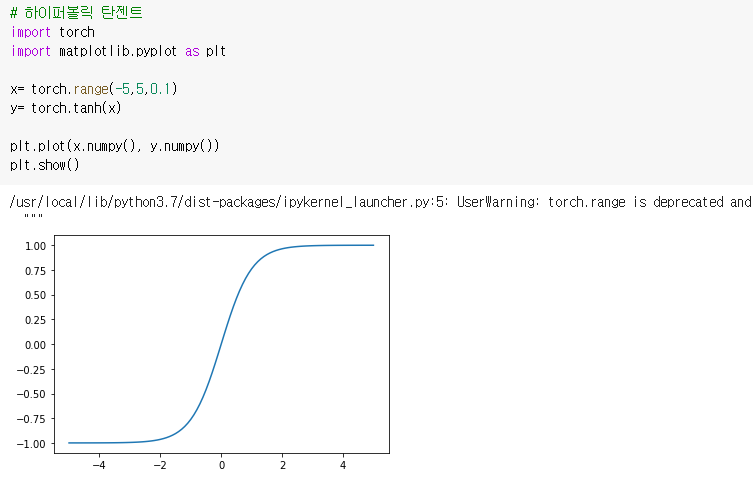
- 위 그래프에서 볼 수 있다싶이 시그모이드 함수의 출력값이 0-1이었던 반면 탄젠트 함수의 출력값은 -1에서 1값을 갖는다. 즉 기울기가 양수와 음수 모두 나올 수 있기 때문에 시그모이드 함수보다 학습 효율성이 뛰어나다.
- -1에서 1에 y가 분포하고 있어 시그모이드 함수보다 그 범위가 넓어 출력값의 변화폭이 크다. 따라서 그레디언트 소실증상도 시그모이드에 비해 덜한 편이다.
- 그럼에도 탄젠트함수 역시 그 범위가 그닥 많이 크지는 않다. 따라서 기울기 소실 문제를 완전히 해결해줄 수는 없다.
ReLU함수는 그레디언트 소실 문제 해결에 도움을 줄 수 있는 다른 활성화함수로 최근 딥러닝 혁신의 상당수를 가능케해준 중요한 활성화 함수이다.
해당 함수에 대해선 다음 포스팅에서 알아보자.
'Data > 머신러닝 & 딥러닝' 카테고리의 다른 글
| 신경망의 기본 구성 요소(6)/ 손실함수 (2) | 2021.07.20 |
|---|---|
| 신경망의 구성요소(5)/ 활성화 함수- 소프트맥스 (0) | 2021.07.20 |
| 신경망의 구성요소 (4)/ 활성화 함수- ReLU (0) | 2021.07.20 |
| 신경망의 기본 구성요소(2)/ 활성화함수- 시그모이드 (0) | 2021.07.19 |
| 신경망의 기본 구성요소 (1)/ 퍼셉트론과 논리게이트, 파이토치 구현 (2) | 2021.07.19 |