수학채널 쑤튜브 영상을 참고했습니다.
▶ 의사역행렬
역행렬은 정사각행렬일 경우 만들어질 수 있다. 행과 열의 수가 다른 경우 역행렬은 만들어질 수 없다. 그러나 이 행렬에 대한 의사역행렬은 만들 수 있다. 의사역행렬은 역행렬과 유사한 행렬을 의미한다.
우선 축소된 svd개념부터 살펴보자. 특이값 분해는 행과 열이 다른 행렬을 직교 행렬 U,V와 주 대각성분이 특이값으로 이뤄진 시그마 행렬의 곱으로 나타내는 것이다. 축소된 특이값 분해는 행렬에서 0으로만 이뤄진(대수적으로 무의미한) 행과 열을 모두 제거하고 나타낸 행렬곱이다.


비가역행렬과 가역행렬에서 축소된 svd는 다음과 같은 shape을 가진다.

- 여기서 시그마 프라임은 모든 대각원소가 0이 아닌 정사각 대각행렬이므로 가역행렬이다.
- u프라임과 v프라임은 full column rank이면서 정사각이기 때문에 직교행렬이다. 즉 가역행렬이다.
따라서 B의 역행렬은 다음과 같이 나타낼 수 있다.

위와 같은 꼴은 A행렬에서도 축소된 특이값 분해를 통해 만들어낼 수 있다. u프라임과 v프라임이 정사각행렬은 아닐순 있지만 특이값 분해를 통해 위와 같은 꼴을 만들어낼 순 있다.
즉 A행렬 같은 경우 역행렬은 아니지만 특이값 분해를 통해 가역행렬의 역행렬꼴과 유사한 역행렬을 만들어낼 수 있다. 이를 의사역행렬이라고 한다.
▷ 의사역행렬로 선형회귀식 찾기
아래와 같이 의사 역행렬을 이용해 베타를 구한 후, 그 베타값을 사용해 Yhat 값을 실제 y값에 근접하도록 하는 선형회귀식을 찾을 수 있다.

이를 파이썬으로 구현해보았다.
우선 scikit learn의 선형회귀함수를 쓰면 다음과 같은 결과가 나온다.

그리고 의사역행렬을 통해 풀어주면 다음과 같은 결과가 나온다.

거의 동일한 값을 산출하는 것을 볼 수 있다.
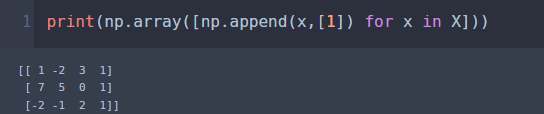
의사역행렬을 사용해 sklearn의 값과 동일한 값을 내고자 할 때 주의할 점은 다음 코드와 같이 x행렬에 y절편을 추가한 후 연산해야한다는 것이다. 그 이유는 sklearn의 경우 y절편을 자동으로 더해서 추정해주기 때문이다.
'수학 > 선형대수학' 카테고리의 다른 글
| 직선, 평면 벡터방정식 (0) | 2021.07.14 |
|---|---|
| 전치행렬 (1) | 2021.07.13 |
| 코사인 유사도(cosine similarity)/ 파이썬 구현 (0) | 2021.07.13 |
| 역행렬과 역행렬의 특징/ 행렬식, (비)가역행렬 (3) | 2021.07.12 |
| 연립 일차 방정식, 행렬로 풀기/ 가우스조던 소거법, 역행렬 (0) | 2021.07.12 |